Нейронная сеть — введение
Принцип обучения многослойной нейронной сети с помощью алгоритма обратного распространения

Рассмотрим процесс обучения нейронной сети с использованием алгоритма обратного распространения ошибки (backpropagation).

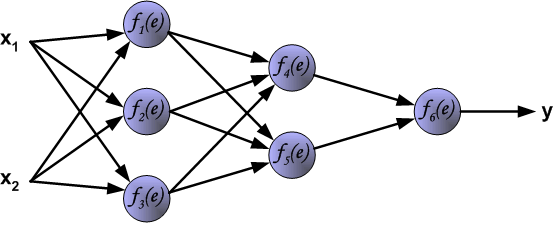
Для иллюстрации этого процесса используем нейронную сеть состоящую из трёх слоёв и имеющую два входа и один выход:

здесь, автор считает слои по-другому и не учитывает «2 нейрона» входного слоя

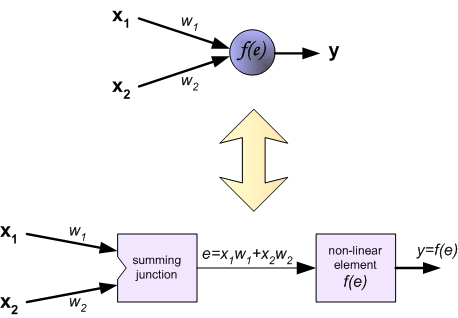
Каждый нейрон состоит из двух элементов.
Первый элемент – дендриты — добавляют весовые коэффициенты ко входным сигналам.
Второй элемент – тело — реализует нелинейную функцию, т.н. функцию активации нейрона.
Сигнал е – это взвешенная сумма входных сигналов

у = f (е)

— выходной сигнал нейрона.


Чтобы обучить нейронную сеть мы должны подготовить обучающие данные(примеры).
В нашем случае, тренировочные данные состоят из входных сигналов (х1 и х2) и желаемого результата z.
Обучение – это последовательность итераций (повторений).
В каждой итерации весовые коэффициенты нейронов подгоняются с использованием новых данных из тренировочных примеров.
Изменение весовых коэффициентов и составляют суть алгоритма, описанного ниже.

Каждый шаг обучения начинается с воздействия входных сигналов из тренировочных примеров. После этого мы можем определить значения выходных сигналов для всех нейронов в каждом слое сети.
Иллюстрации ниже показывают, как сигнал распространяется по сети.
Символы W(Xm)n представляют вес связи между сетевым входом Xm и нейрона n во входном слое.
Символы y(n) представляют выходной сигнал нейрона n.




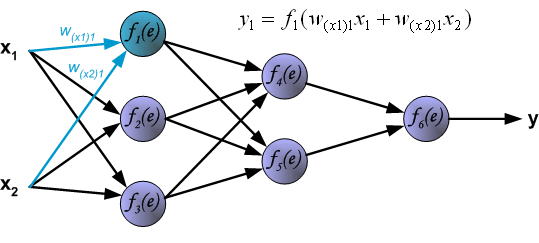
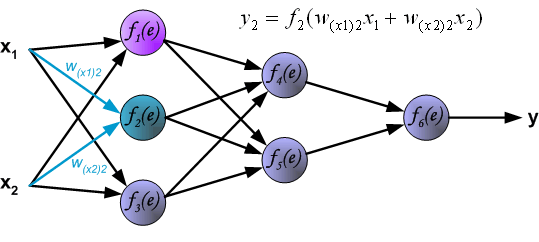
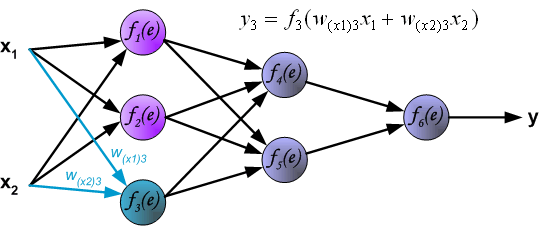
Распространение сигнала через скрытый слой.
Символы Wmn представляют весовые множители связей между выходом нейрона m и входом нейрона n в следующем слое.


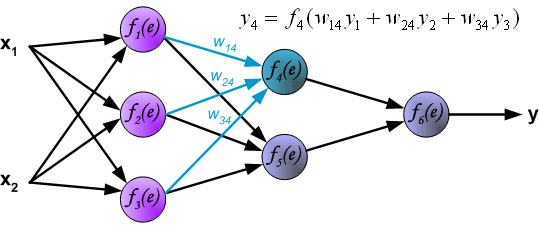
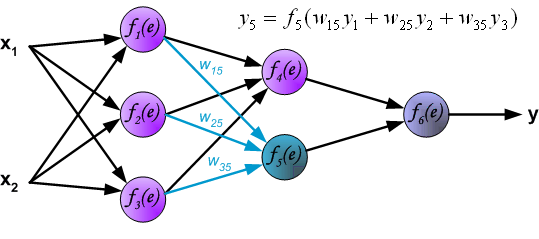
Распространение сигнала через выходной слой

На следующем шаге алгоритма, выходной сигнала сети y сравнивается с желаемым выходным сигналом z, который хранится в тренировочных данных.
Разница между этими двумя сигналами называется ошибкой d выходного слоя сети.


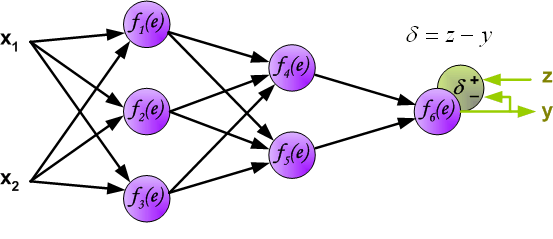
Невозможно непосредственно вычислить сигнал ошибки для внутренних нейронов, потому что выходные значения этих нейронов, неизвестны.
На протяжении многих лет был неизвестен эффективный метод для обучения многослойной сети.
Только в середине восьмидесятых годов был разработан алгоритм обратного распространения ошибки.
Идея заключается в распространении сигнала ошибки d (вычисленного в шаге обучения) обратно на все нейроны, чьи выходные сигналы были входящими для последнего нейрона.


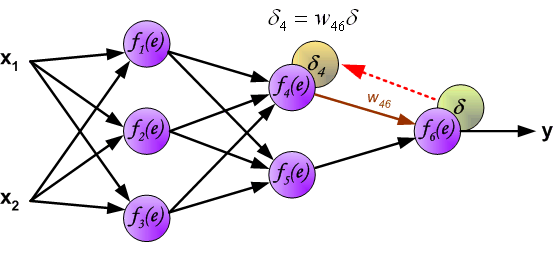
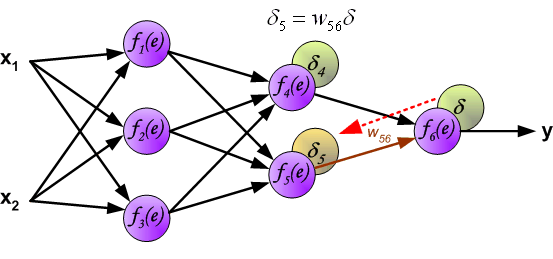
Весовые коэффициенты Wmn, используемые для обратного распространения ошибки, равны тем же коэффициентам, что использовались во время вычисления выходного сигнала. Только изменяется направление потока данных (сигналы передаются от выхода ко входу).
Этот процесс повторяется для всех слоёв сети. Если ошибка пришла от нескольких нейронов — она суммируются:



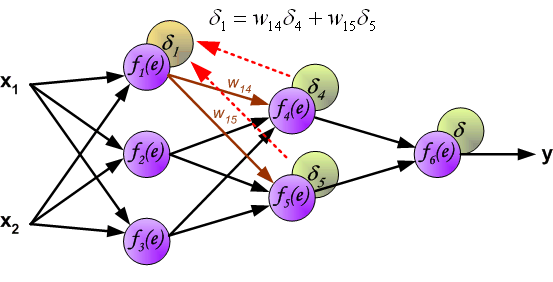
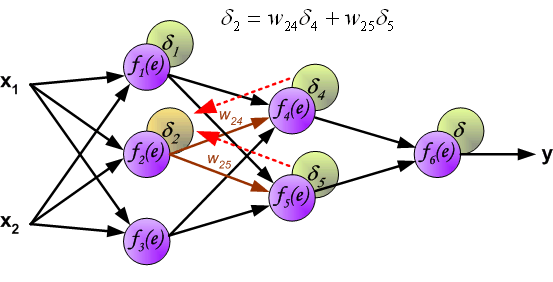
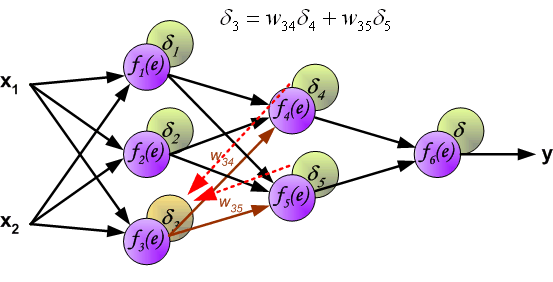
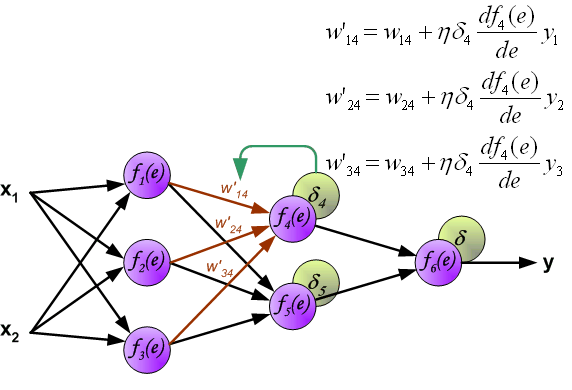
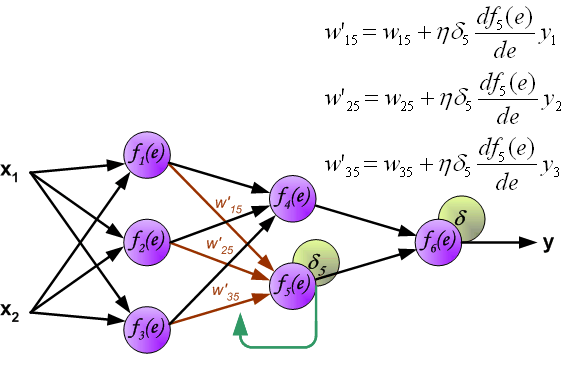
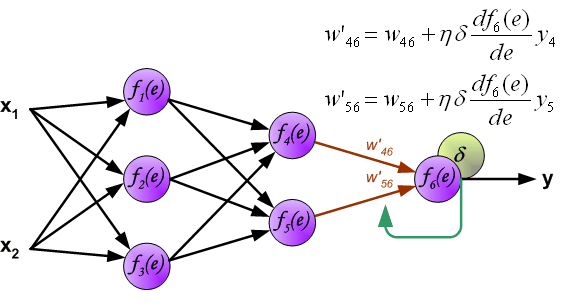
Когда вычисляется величина ошибки сигнала для каждого нейрона – можно скорректировать весовые коэффициенты каждого узла ввода(дендрита) нейрона.
В формулах ниже df(e)/de — является производной от функции активации нейрона (чьи весовые коэффициенты корректируются).

как помним, для активационной функции типа сигмоид

           1
S(x) = -----------
       1 + exp(-x)

производная выражается через саму функцию:

S'(x) = S(x)*(1 - S(x))

, что позволяет существенно сократить вычислительную сложность метода обратного распространения ошибки.

Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.

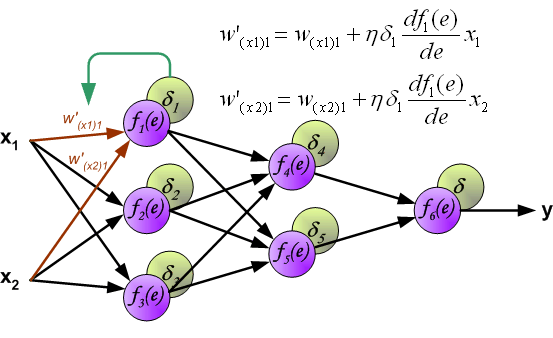
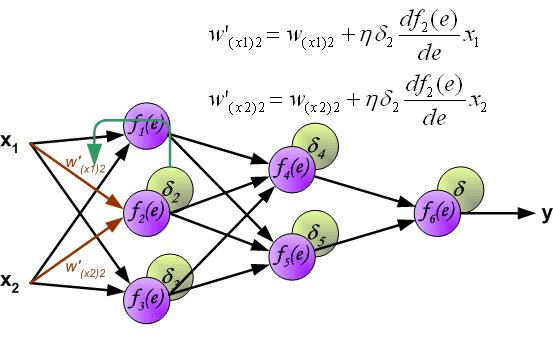
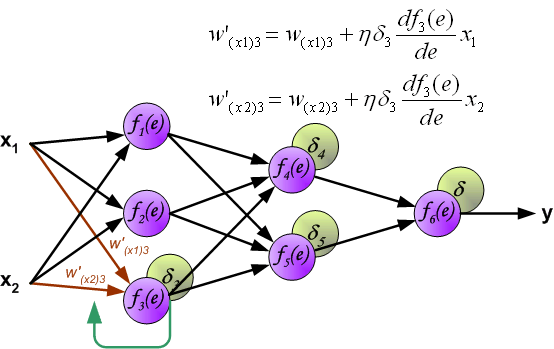
Коэффициент h влияет на скорость обучения сети.
Есть несколько методов для выбора этого параметра.
Первый способ — начать учебный процесс с большим значением параметра h. Во время коррекции весовых коэффициентов, параметр постепенно уменьшают.
Второй — более сложный метод обучения, начинается с малым значением параметра h. В процессе обучения параметр увеличивается, а затем вновь уменьшается на завершающей стадии обучения.
Начало учебного процесса с низким значением параметра h позволяет определить знак весовых коэффициентов.

продолжение следует...

Ссылки
Оригинал статьи (на английском)
http://ru.wikipedia.org/wiki/Метод_обратного_распространения_ошибки
en.wikipedia.org/wiki/Backpropagation
Нейросеть в 11 строчек на Python
An overview of gradient descent optimization algorithms

По теме
Нейронная сеть — введение
Пример работы самоорганизующейся инкрементной нейронной сети SOINN